
Fuvest - 1ª fase
O paralelepípedo reto-retângulo ABCDEFGH, representado na figura, tem medida dos lados AB = 4, BC = 2 e BF = 2.
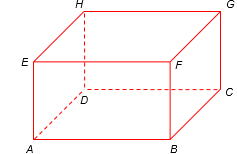
O seno do ângulo HÂF é igual a
| a) |
|
| b) |
|
| c) |
|
| d) |
|
| e) |
|
Seja θ a medida do ângulo HÂF. Construindo o triângulo HAF, temos que:
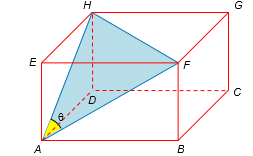
Vamos calcular as medidas dos lados do triângulo HAF. Para tanto, observemos que, sendo ABCDEFGH paralelepípedo reto-retângulo, os triângulos EAF, EHF e EAH são todos triângulos retângulos em E.
Assim:
A partir daqui, podemos apontar dois modos para determinar o seno do ângulo HÂF.
Primeiro modo:
Aplicando o teorema dos cossenos no triângulo HAF, segue que:
..
Da relação fundamental da Trigonometria, vem que:
Sendo θ a medida do ângulo interno de um triângulo, temos que
, de modo que
. Assim, ficamos com:
Segundo modo:
Como
, o triângulo HAF é isósceles. Assim, a altura relativa ao lado
será dada pelo segmento
, onde M é o ponto médio do lado
. Temos a figura:
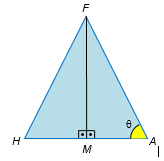
Sendo
, pelo teorema de Pitágoras no triângulo retângulo AMF vem que:
Assim:
João tem para comprar canetas em 3 lojas. Na loja A, as canetas são vendidas em dúzias, cada dúzia custa e há apenas 2 dúzias em estoque. Na loja B, as canetas são vendidas em pares, cada par custa e há 10 pares em estoque. Na loja C, as canetas são vendidas avulsas, cada caneta custa e há 25 canetas em estoque. O maior número de canetas que João pode comprar nas lojas A, B e C utilizando no máximo é igual a
| a) |
46
|
| b) |
45
|
| c) |
44
|
| d) |
43
|
| e) |
42
|
A loja A vende uma dúzia de canetas por R$40,00, sendo assim, cada caneta nessa loja custa, aproximadamente, R$3,33. Já a loja B vende par de canetas por R$7,60, o que significa um custo de R$3,80 por caneta. Por fim, a loja C vende cada caneta avulsa por R$3,20.
Como deseja-se maximizar a quantidade possível de canetas a se comprar, a intuição nos levaria a crer que o melhor caso seria comprar o máximo possível de canetas na loja que vende o pacote com valor médio por caneta mais barato (loja C), e depois comprar a maior quantidade possível de canetas na loja com o segundo melhor preço (loja A). Porém, tal raciocínio não leva em consideração o dinheiro restante após a compra. Como mostra o quadro a seguir, deixar de comprar algumas canetas na loja C pode fazer com que sobre dinheiro para um pacote maior de canetas em outra loja, resultando em um total maior de canetas compradas.
Há que perceber ainda que não existe vantagem em se trocar a compra de duas canetas na loja C por um pacote de duas canetas da loja B. E também não há vantagem em se trocar a compra de uma dúzia de canetas na loja A por seis pacotes de duas canetas cada na loja B. Assim, levando em consideração que a loja C (que vende as canetas pelo menor preço) possui apenas 25 unidades, totalizando R$80,00, é possível efetuar a compra de pelo menos uma dúzia de canetas na loja A. Portanto, o quadro a seguir mostra apenas casos mais vantajosos em que são compradas uma ou duas dúzias de canetas na loja A.
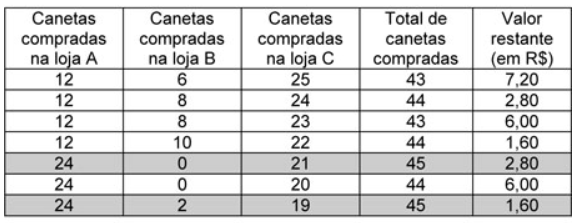
Concluímos então que o máximo de canetas possíveis de serem compradas é 45.
Cláudia, Paulo, Rodrigo e Ana brincam entre si de amigo-secreto (ou amigo-oculto). Cada nome é escrito em um pedaço de papel, que é colocado em uma urna, e cada participante retira um deles ao acaso. A probabilidade de que nenhum participante retire seu próprio nome é
| a) |
|
| b) |
|
| c) |
|
| d) |
|
| e) |
|
Primeira Resolução:
Vamos calcular a quantidade de casos em que:
apenas um participante tira seu próprio nome;
apenas dois dos participantes tiram seus respectivos nomes;
todos os quatro participantes tirem seus respectivos nomes.
Note que não há como exatamente três participantes retirarem seus respectivos nomes, pois, o quarto certamente também deveria pegar seu próprio nome.
Denotemos os participantes por A (Ana), C (Cláudia), P (Paula) e R (Rodrigo).
I. Fixemos o caso em que A retira seu próprio nome. Assim, C não poderá retirar C, sobrando-lhe duas opções: P ou R. Caso C retire R, então R não poderá retirar C, uma vez que sobraria para P apenas seu próprio nome. O mesmo ocorre se C tirar P. Nesse caso, P deve retirar R.
Assim, para cada participante fixado retirando seu próprio nome, há dois casos em que ele é o único a fazer isso, totalizando 4 × 2 = 8 possibilidades em que apenas um participante retira o próprio nome.
II. Se fixamos dois participantes retirando seus respectivos nomes, resta que os outros dois retirem o nome um do outro. Assim, o número de possibilidades deste caso é igual ao número de possibilidades de se escolher dois entre os quatro participantes, que é:
.
III. Só há uma maneira de que todos os quatro participantes retirem cada um o seu respectivo nome.
Totalizamos assim 8 + 6 + 1 = 15 casos que não são pertinentes à brincadeira. Como há 4! = 24 casos possíveis, os casos em que estamos interessados são 24 − 15 = 9. Portanto, a probabilidade p procurada é:
.
Segunda Resolução:
O exercício lida com um problema que em Análise Combinatória é chamado de permutação caótica (ou desarranjo), no qual queremos calcular a quantidade de permutações de n elementos em que, após a permutação, nenhum deles ocupe sua posição inicial.
Seja dn o número de possíveis desarranjos de n elementos. Podemos estabelecer inicialmente que:
, pois é impossível permutar um único elemento sem que ele ocupe seu lugar inicial;
, uma vez que o único desarranjo possível é trocar a posição dos dois elementos.
Já para qualquer n natural tal que
, selecionamos um elemento qualquer, por exemplo o que ocupava a primeira posição, e escolhemos a nova posição dele: temos n − 1 opções para essa escolha, já que só não podemos colocá-lo em sua posição original. A partir disso, seja k a posição onde ele foi colocado. Temos que:
se o elemento que estava na posição k foi para a posição 1, temos
maneiras de permutar os demais;
se o elemento que estava na posição k não foi para a posição 1, temos
maneiras de permutar os demais (pensando que ao invés de não querer o elemento que estava na posição k em sua posição original, agora não queremos ele na posição 1).
Temos aqui:
Assim:
Como o total de permutações entre os quatro amigos é
, a probabilidade de que nenhum deles tire o próprio nome é
.
Terceira Resolução:
O total de permutações é dado por
.
O número de permutações em que pelo menos um dos participantes tirou seu próprio nome pode ser calculado pelo princípio da inclusão e exclusão:
,
onde inicialmente incluímos os casos em que um elemento está fixo e permutando os demais, em seguida descontamos aqueles casos em que dois ficaram fixos, permutando os demais, em seguida incluímos os casos em que três ficaram fixos, permutando os demais, etc.
Assim, o total de casos em que nenhum elemento ficou fixo é dada por:
Logo, a probabilidade de que nenhum deles tire o próprio nome é:
.
O retângulo , representado na figura, tem lados de comprimento e . O ponto pertence ao lado e . Os pontos , e pertencem aos lados , e , respectivamente. O segmento é paralelo a e intercepta no ponto . O segmento é paralelo a .
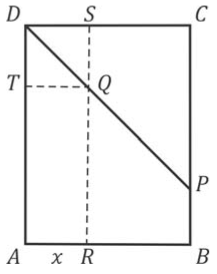
Sendo o comprimento de , o maior valor da soma das áreas do retângulo , do triângulo e do triângulo , para variando no intervalo aberto , é
| a) |
|
| b) |
|
| c) |
|
| d) |
|
| e) |
|
Devemos calcular o valor máximo da soma das áreas:
Para isso, observe que o
é retângulo e isósceles pois
e além disso:
Logo, como
temos que
de onde segue
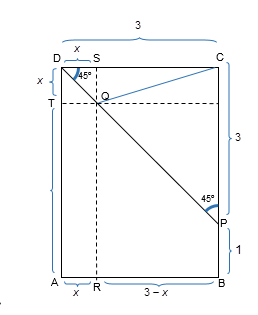
Desta forma, conseguimos obter as áreas:
e
Agora, para obter
, note que sua altura relativa à base PC tem mesma medida que RB, logo
Como
é uma função quadrática, seu gráfico é dado por uma parábola (neste caso com concavidade para baixo, pois coeficiente do termo quadrático é negativo). Portanto podemos determinar sua área máxima através do vértice (
).
Assim,
OBS: Note que:
, que pertence ao intervalo aberto estipulado pelo enunciado.
Na figura, o retângulo tem lados de comprimento e . Sejam o ponto médio do lado e o ponto médio do lado . Os segmentos e interceptam o segmento nos pontos E e F, respectivamente.
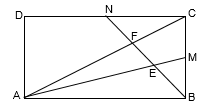
A área do triângulo
é igual a
| a) |
|
| b) |
|
| c) |
|
| d) |
|
| e) |
|
Para resolver o exercício, vamos considerar o prolongamento dos segmentos e , até o ponto de interseção
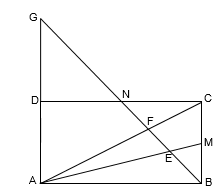
Como possui metade do comprimento de e , segue que segmento mede 4 (o dobro do segmento ).
Note que os triângulos e são semelhantes (caso AA). Sendo e as alturas dos triângulos e , respectivamente, como e , concluímos que (a razão entre os lados de dois triângulos congruentes é igual a razão entre suas alturas). Porém, assim, a área do triângulo é:
Por outro lado, os triângulos e também são semelhantes (caso AA). Sendo assim, como suas bases são, respectivamente, 4 e 2, suas alturas e estão relacionadas por . Logo,
Portanto, a área do triângulo é
Agora, note que o triângulo possui base e altura iguais a 2, e portanto,
Mas, sua área é igual a soma das áreas dos triângulos e , com a área do quadrilátero , ou seja,
Por fim, note que a área do triângulo é a área do triângulo menos a área do quadrilátero . O triângulo possui base 1 e altura 4, portanto,
Então,
Considere as funções e , em que o domínio de é o conjunto dos números reais e o domínio de é o conjunto dos números reais maiores do que 0. Seja , em que . Então, é igual a
| a) |
4
|
| b) |
8
|
| c) |
12
|
| d) |
16
|
| e) |
20
|
Temos que:
Assim:
Sendo:
,
segue que:
O polinômio possui uma raiz complexa cuja parte imaginária é positiva. A parte real de é igual a
| a) |
−11
|
| b) |
−7
|
| c) |
9
|
| d) |
10
|
| e) |
12
|
Dado o polinômio
, cujos coeficientes são todos inteiros, então, pelo teorema das raízes racionais, temos que se
admite alguma raiz racional do tipo
, com p e q inteiros primos entre si, então p é divisor de −5 (termo independente) e q é divisor de 1 (coeficiente do termo dominante). Deste modo, as possíveis raízes racionais seriam
e
.
Como a soma dos coeficiente de
é nula, então 1 é raiz de
. Logo, utilizando o dispositivo prático de Briot-Ruffini, temos:
Deste modo, fatorando
:
Para encontrarmos as outras duas raízes complexas, fazemos:
Logo, sendo
um número complexo de parte imaginária positiva, ficamos com:
E,
Portanto,
Um reservatório de água tem o formato de um cone circular reto. O diâmetro de sua base (que está apoiada sobre o chão horizontal) é igual a 8 m. Sua altura é igual a 12 m. A partir de um instante em que o reservatório está completamente vazio, inicia-se seu enchimento com água a uma vazão constante de 500 litros por minuto. O tempo gasto para que o nível da água atinja metade da altura do reservatório é de, aproximadamente,
|
Dados: é aproximadamente 3,14. O volume de um cone circular reto de altura e raio da base é . |
| a) |
4 horas e 50 minutos.
|
| b) |
5 horas e 20 minutos.
|
| c) |
5 horas e 50 minutos.
|
| d) |
6 horas e 20 minutos.
|
| e) |
6 horas e 50 minutos.
|
Observe a figura abaixo
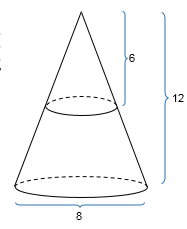
Note que, o cone maior e o cone menor são semelhantes, logo, sendo v o volume do cone menor e V o volume do cone maior, temos:
Assim, o volume a ser preenchido pela água é dado por um tronco de cone, que é a diferença entre o volume do cone maior e o volume do cone menor, ou seja:
No enunciado é dado , então:
Lembrando que a vazão é dada em litros por minuto e que:
Segue que:
Agora, basta dividirmos o volume pela vazão para obtermos o tempo gasto.
Duas circunferências com raio 1 e 2 têm centros no primeiro quadrante do plano cartesiano e ambas tangenciam os dois eixos coordenados. Essas circunferências se interceptam em dois pontos distintos de coordenadas (x1,y1) e (x2,y2).
O valor de
é igual a:
| a) |
|
| b) |
|
| c) |
|
| d) |
|
| e) |
|
O desenho correspondente à situação descrita é:
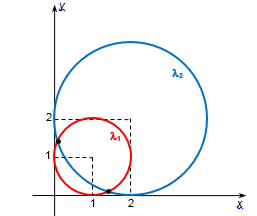
As equações das circunferências λ1 e λ2 são:
Os pontos em comum às duas circunferências são pontos que devem
satisfazer simultaneamente as equações das circunferências, ou seja, devem ser as soluções do sistema:
Subtraindo membro a membro uma equação da outra, vem que:
Assim, sendo (x1,y1) e (x2,y2) coordenadas de pontos que satisfazem essa igualdade, segue que:
Uma quantidade fixa de um gás ideal é mantida a temperatura constante, e seu volume varia com o tempo de acordo com a seguinte fórmula:
, ,
em que t é medido em horas e V(t) é medido em m3. A pressão máxima do gás no intervalo de tempo [0,2] ocorre no instante
| a) |
|
| b) |
|
| c) |
|
| d) |
|
| e) |
|
Pela equação de Clapeyron, se a temperatura é mantida constante, então o produto pressão por volume também será mantido constante. Portanto, a pressão do gás será máxima quando o volume for mínimo.
Sendo o logaritmo em base maior do que 1 uma função estritamente crescente, o volume será mínimo quando o logaritmando for mínimo. Assim, devemos trabalhar com o mínimo da expressão:
para , que será atingido quando o seno atingir seu valor mínimo, que é . Portanto:
, com
Sendo
, devemos fazer
: