
Fuvest - 1ª fase
As figuras representam arranjos de fios longos, retilíneos, paralelos e percorridos por correntes elétricas de mesma intensidade. Os fios estão orientados perpendicularmente ao plano desta página e dispostos segundo os vértices de um quadrado. A única diferença entre os arranjos está no sentido das correntes: os fios são percorridos por correntes que entram () ou saem () do plano da página.
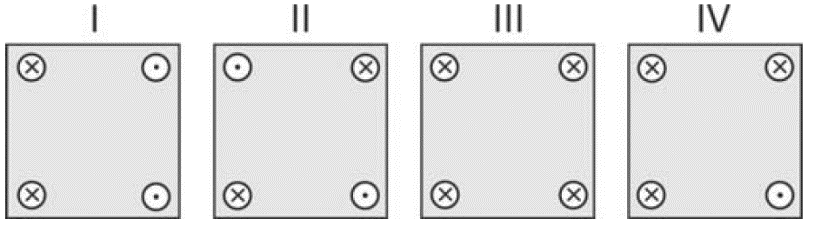
O campo magnético total é nulo no centro do quadrado apenas em
| a) |
I.
|
| b) |
II.
|
| c) |
I e II.
|
| d) |
II e III.
|
| e) |
III e IV.
|
Pala regra da mão direita (o dedão aponta no sentido da corrente e a mão gira no sentido do campo magnético formado pelo fio), temos os seguintes perfis para o campo magnético produzido pelas correntes quando sai e quando entra no plano do papel, respectivamente:

Podemos determinar a direção do campo magnético em um ponto pela reta tangente à linha do campo magnético no ponto de interesse, como ilustrado a seguir (campo magnético em um ponto P):
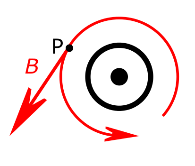
Agora podemos determinar a direção do campo magnético no centro dos quadrados em cada caso.
Começando pela primeira figura:
I
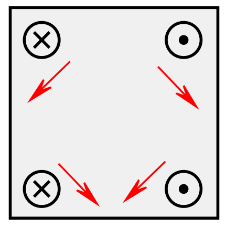
Os campos representados na figura são produzidos no centro do quadrado, entretanto foram representados próximos aos fios que os produziram para ficar mais claro. Somando estes vetores, vemos que a resultante desta soma não é nula:
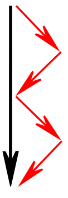
Fazendo o mesmo para as demais figuras:
II
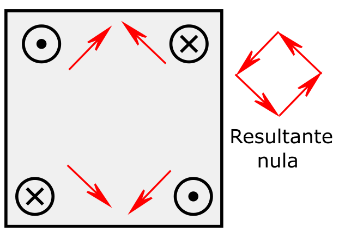
Portanto II produz campo nulo.
III
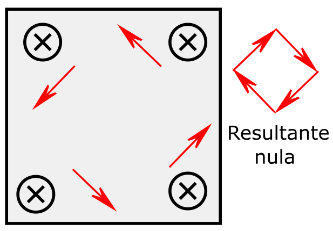
Portanto III produz campo nulo.
IV
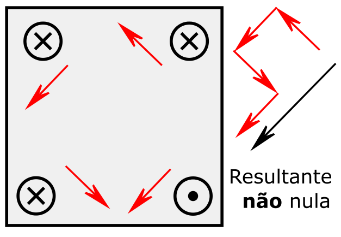
Este último não produz campo nulo. Portanto a resposta é a alternativa D.
Na bateria de um telefone celular e em seu carregador, estão registradas as seguintes especificações:

Com a bateria sendo carregada em uma rede de 127 V, a potência máxima que o carregador pode fornecer e a carga máxima que pode ser armazenada na bateria são, respectivamente, próximas de
| a) |
25,4 W e 5940 C.
|
| b) |
25,4 W e 4,8 C.
|
| c) |
6,5W e 21960 C.
|
| d) |
6,5W e 5940 C.
|
| e) |
6,1W e 4,8 C.
|
A potência de saída é calculada pelo produto da tensão de saída pela corrente de saída:
A carga é dada no enunciado:
Basta convertê-la para coulomb:
A figura representa uma onda harmônica transversal, que se propaga no sentido positivo do eixo x, em dois instantes de tempo: t = 3 s (linha cheia) e t = 7 s (linha tracejada).
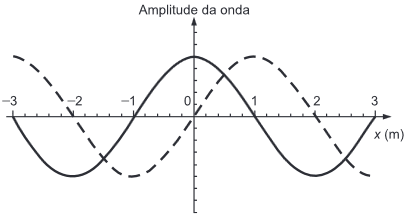
Dentre as alternativas, a que pode corresponder à velocidade de propagação dessa onda é
| a) |
0,14 m/s
|
| b) |
0,25 m/s
|
| c) |
0,33 m/s
|
| d) |
1,00 m/s
|
| e) |
2,00 m/s
|
Pela figura do enunciado, vemos que a distância que a onda percorre, supondo que esta distância seja menor que um comprimento de onda, é
.
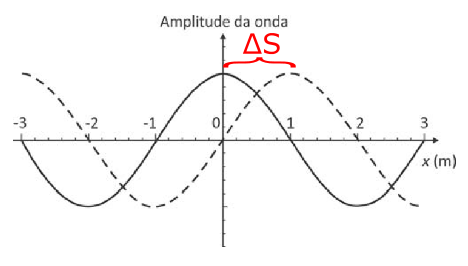
Como para percorrer esta distância foi um tempo
, então a velocidade da onda será:
Obs: como um caso geral, caso em que a onda percorre uma distância maior que um comprimento de onda, podemos escrever que
Sendo n um número inteiro que corresponde à quantos comprimentos de onda a onda teria percorrido a mais que o
indicado na figura acima (n = 0, 1, 2, ...). Portanto a velocidade seria:
Note que a única resposta possível é para n = 0.
Reatores nucleares não são exclusivamente criações humanas. No período pré-cambriano, funcionou na região de Oklo, África, durante centenas de milhares de anos, um reator nuclear natural, tendo como combustível um isótopo do urânio.
Para que tal reator nuclear natural pudesse funcionar, seria necessário que a razão entre a quantidade do isótopo físsil (235U) e a do urânio 238U fosse cerca de 3%. Esse é o enriquecimento utilizado na maioria dos reatores nucleares, refrigerados a água, desenvolvidos pelo homem.
O 235U decai mais rapidamente que o 238U; na Terra, atualmente, a fração do isótopo 235U, em relação ao 238U, é cerca de 0,7%. Com base nessas informações e nos dados fornecidos, pode-se estimar que o reator natural tenha estado em operação há

| a) |
a) 1,2 × 107 anos. |
| b) |
b) 1,6 × 108 anos. |
| c) |
c) 2,0 × 109 anos. |
| d) |
d) 2,4 × 1010 anos. |
| e) |
e) 2,8 × 1011 anos. |
Dados do enunciado:
Sendo
,
,
e
as massas, respectivamente, inicial do urânio 235, inicial do urânio 238, atual do urânio 235 e atual do urânio 238.
Usando a equação dada no enunciado, temos:
Substituindo estas equações no sistema de cima, dividindo a equação de baixo pela de cima e substituindo os dados do enunciado, temos:
Aplicando a função log em ambos os lados da equação, usando o dado do “Note e adote” e usando suas propriedades, temos:
Em uma aula de laboratório de física, utilizando-se o arranjo experimental esquematizado na figura, foi medido o índice de refração de um material sintético chamado poliestireno. Nessa experiência, radiação eletromagnética, proveniente de um gerador de micro-ondas, propaga-se no ar e incide perpendicularmente em um dos lados de um bloco de poliestireno, cuja seção reta é um triângulo retângulo, que tem um dos ângulos medindo 25º, conforme a figura. Um detetor de micro-ondas indica que a radiação eletromagnética sai do bloco propagando-se no ar em uma direção que forma um ângulo de 15º com a de incidência.
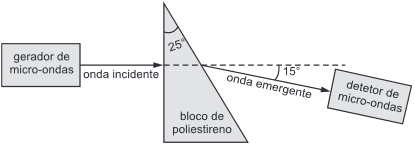
A partir desse resultado, conclui-se que o índice de refração do poliestireno em relação ao ar para essa micro-onda é, aproximadamente,
NOTE E ADOTE: Índice de refração do ar: 1,0
| a) |
1,3
|
| b) |
1,5
|
| c) |
1,7
|
| d) |
2,0
|
| e) |
2,2
|
A figura abaixo ilustra a situação descrita pelo enunciado.
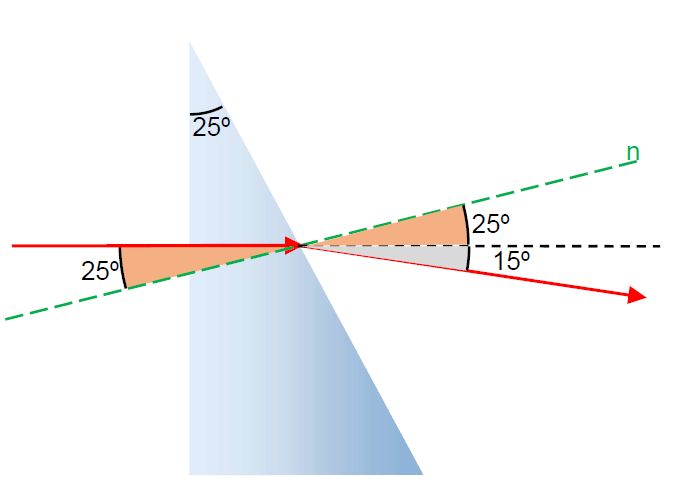
Por semelhança de triângulos, concluímos que o ângulo de incidência é de 25º (ângulo entre raio incidente e a reta normal, desenhada em verde na figura acima). Sabendo que o desvio angular é de 15º, então podemos, facilmente, verificar que o ângulo de refração é de 40º (ângulo entre o raio emergente e a reta normal).
Sabendo os ângulos de incidência e refração, basta usarmos a lei de Snell-Descartes para encontrarmos o índice de refração do poliestireno.
.
No início do século XX, Pierre Curie e colaboradores, em uma experiência para determinar características do recém-descoberto elemento químico rádio, colocaram uma pequena quantidade desse material em um calorímetro e verificaram que 1,30 grama de água líquida ia do ponto de congelamento ao ponto de ebulição em uma hora. A potência média liberada pelo rádio nesse período de tempo foi, aproximadamente,
|
NOTE E ADOTE: Calor específico da água: 1cal/(gºC) 1 cal = 4 J Temperatura de congelamento da água: 0 ºC Temperatura de ebulição da água: 100 ºC Considere que toda a energia emitida pelo rádio foi absorvida pela água e empregada exclusivamente para elevar sua temperatura. |
| a) |
0,06 W
|
| b) |
0,10 W
|
| c) |
0,14W
|
| d) |
0,18 W
|
| e) |
0,22 W
|
Supondo uma situação ideal, podemos dizer que toda energia fornecida para o aquecimento da água veio do elemento Ra e que toda energia liberada pelo Rádio foi absorvida pela água, ou seja, trata-se de uma situação com rendimento de 100%.
A energia necessária para o aquecimento de 1,3 g de água de 0ºC a 100ºC é dada por
.
Assumindo que toda essa energia veio do Rádio e sabendo que o experimento durou 1 h temos que a potência média liberada por ele é dada por
.
Um objeto metálico, X, eletricamente isolado, tem carga negativa 5,0 x 10–12 C. Um segundo objeto metálico, Y, neutro, mantido em contato com a Terra, é aproximado do primeiro e ocorre uma faísca entre ambos, sem que eles se toquem. A duração da faísca é 0,5 s e sua intensidade é 10–11 A. No final desse processo, as cargas elétricas totais dos objetos X e Y são, respectivamente,
| a) |
zero e zero.
|
| b) |
zero e – 5,0 x 10–12 C.
|
| c) |
– 2,5 x 10–12 C e – 2,5x 10–12 C.
|
| d) |
– 2,5 x 10–12 C e + 2,5x 10–12 C.
|
| e) |
+ 5,0 x 10–12 C e zero.
|
A figura abaixo ilustra a situação descrita no enunciado. Note que a carga do objeto Y deverá ser nula, já que este permanece aterrado todo o tempo, isso já nos permite eliminar as alternativas B, C e D.
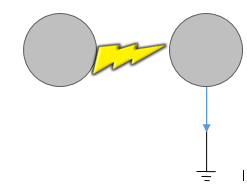
A carga transferida do objeto X (carregado) para o objeto Y (neutro) é dada por
Então o corpo X liberou toda a carga que tinha em excesso para o Corpo Y. No entanto o corpo Y está aterrado e todo o excesso de carga que recebe é transferido para a terra. Sendo assim os dois condutores estarão neutros (carga nula) no fim do experimento.
Na estratosfera, há um ciclo constante de criação e destruição do ozônio. A equação que representa a destruição do ozônio pela ação da luz ultravioleta solar (UV) é
O gráfico representa a energia potencial de ligação entre um dos átomos de oxigênio que constitui a molécula de O3 e os outros dois, como função da distância de separação r.
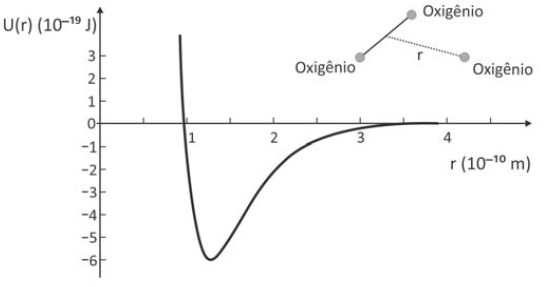
A frequência dos fótons da luz ultravioleta que corresponde à energia de quebra de uma ligação da molécula de ozônio para formar uma molécula de O2 e um átomo de oxigênio é, aproximadamente,
| NOTE E ADOTE: é a energia do fóton. é a frequência da luz. Constante de Planck, |
| a) |
1x1015 Hz
|
| b) |
2x1015 Hz
|
| c) |
3x1015 Hz
|
| d) |
4x1015 Hz
|
| e) |
5x1015 Hz
|
A formação de uma molécula constituída por n átomos ocorre devido a força elétrica entre eles. Sendo cada átomo formado por uma eletrosfera (negativa) e por um núcleo (positivo), teremos forças de atração e repulsão entre os átomos. Pelo princípio da superposição podemos analisar a interação par a par dos átomos e por fim encontrar a interação total do sistema sobre si mesmo.
O esquema a seguir ajuda a entender quando ocorrem forças de atração e repulsão
Em vez de estudarmos as forças sobre cada átomo, é comum estudarmos a energia potencial de cada um, isso é vantajoso pelo fato de a energia ser uma grandeza escalar (diferente da força que é vetorial). Encontrar a energia potencial de um sistema de 3 átomos não é uma tarefa trivial, e está fora do escopo do ensino médio, sendo assim iremos nos restringir à análise do gráfico fornecido pelo enunciado.
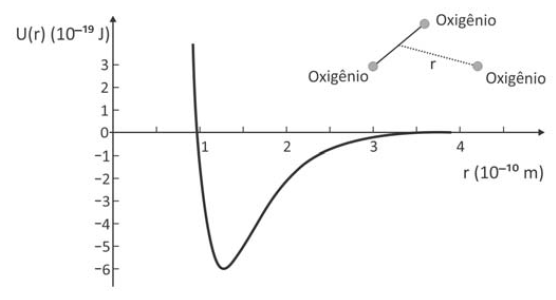
Este gráfico representa a energia potencial de um átomo de oxigênio em função de sua distância em relação ao centro de massa do outro par de oxigênio contido na molécula de Ozônio.
Agora, é muito importante, que consigamos analisar que tipo de força (atrativa ou repulsiva) atua sobre o átomo de acordo com o gráfico fornecido. Para isso vamos usar o princípio que diz que um sistema físico isolado sempre tende para a situação de menor energia.
Quando o átomo de oxigênio está na posição ele está na posição de menor energia possível, portanto está em equilíbrio.
Se o átomo estive à esquerda dessa posição, ou seja , então ele será “empurrado” de volta a posição de equilíbrio, o que significa que ele será repelido pelo resto do conjunto.
Se o átomo estiver à direita do ponto de equilíbrio, ou seja ele será “puxado” de volta para a posição de equilíbrio, o que siginifica que ele será atraído pelo resto do conjunto.
Vamos resumir essas informações:
Agora note que se o átomo estiver distante do resto do conjunto, ou seja, a uma distância maior do que então ele “não sabe mais” que existe um ponto de energia mínima, ele está numa região de energia constante e igual a zero. De fato, podemos dizer que este átomo está tão longe do resto do conjunto que a interação eletrostática não existe mais, sendo assim dizemos que o átomo está livre.
Dito isso podemos dizer que para romper a molécula de Ozônio, liberando um átomo de oxigênio, devemos tirar ele da posição de equilíbrio, na qual sua energia potencial é , para uma posição maior do que , onde sua energia potencial é nula (região onde o átomo está livre).
Sendo assim a menor energia necessária para romper a molécula de Ozônio é
.
Agora, supondo que 1 (um) fóton é responsável pela quebra de 1 (uma) molécula, então a energia desse fóton deve ser de .
Finalmente para encontrar a energia do fóton contido no feixe de luz UV para a quebra do Ozônio temos
.
Dependendo do pH do solo, os nutrientes nele existentes podem sofrer transformações químicas que dificultam sua absorção pelas plantas. O quadro mostra algumas dessas transformações, em função do pH do solo.
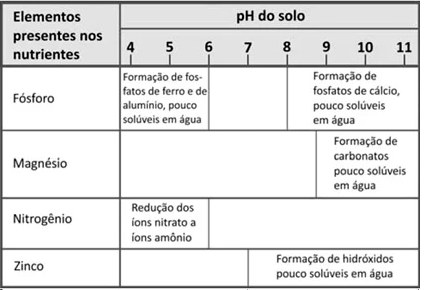
Para que o solo possa fornecer todos os elementos citados na tabela, o seu pH deverá estar entre
| a) |
4 e 6.
|
| b) |
4 e 8.
|
| c) |
6 e 7.
|
| d) |
6 e 11.
|
| e) |
8,5 e 11.
|
a) Incorreta. Entre os pH 4 e 6, os fosfatos de ferro e de alumínio são poucos solúveis em água, o que dificulta a absorção do fósforo e, além disso, ocorre a redução dos íons nitrato a íons amônio, o que dificulta a absorção do nitrogênio.
b) Incorreta. Entre os pH 4 e 8, além dos fosfatos pouco solúveis e do nitrogênio na forma de amônio, teremos a formação do hidróxido de zinco pouco solúvel
c) Correta. Pela tabela proposta percebe-se que a faixa de pH em que não ocorre nenhuma restrição a absorção dos diferentes elementos é entre os pH 6 e 7, onde eles estão em uma forma solúvel.
d) Incorreta. Entre os pH 6 e 11, o fosfato de cálcio, o carbonato de magnésio e o hidróxido de zinco são poucos solúveis.
e) Incorreta. Entre os pH 8,5 e 11, novamente teremos o fosfato de cálcio, o carbonato de magnésio e o hidróxido de zinco são poucos solúveis.
Em ambientes naturais e na presença de água e gás oxigênio, a pirita, um mineral composto principalmente por dissulfeto de ferro (FeS2), sofre processos de intemperismo, o que envolve transformações químicas que acontecem ao longo do tempo.
Um desses processos pode ser descrito pelas transformações sucessivas, representadas pelas seguintes equações químicas:
2 FeS2(s) + 7 O2 (g) + 2 H2O (l) → 2 Fe2+ (aq) + 4 (aq) + 4 H+ (aq)
2 Fe2+ (aq) + ½ O2 (g) + 2 H+ (aq) → 2 Fe3+ (aq) + H2O (l)
2 Fe3+ (aq) + 6 H2O (l) → 2 Fe(OH)3 (s) + 6 H+ (aq)
Considerando a equação química que representa a transformação global desse processo, as lacunas da frase “No intemperismo sofrido pela pirita, a razão entre as quantidades de matéria do FeS2 (s) e do O2 (g) é __________, e, durante o processo, o pH do solo __________” podem ser corretamente preenchidas por
| a) |
1/4; diminui.
|
| b) |
1/4; não se altera.
|
| c) |
2/15; aumenta.
|
| d) |
4/15; diminui.
|
| e) |
4/15; não se altera.
|
A pirita (FeS2) é um mineral que submetido ao intemperismo, na presença de água e oxigênio, apresenta as seguintes equações químicas:
A proporção, em quantidade de matéria (n), entre a pirita (FeS2) com oxigênio (O2) é a seguinte:
Na análise da equação global observa-se a liberação de H+(aq), o que deve aumentar a concentração de H+(aq) em solução, provocando uma diminuição do pH como indicado na expressão do potencial hidrogeniônico (pH): pH = – log [H+].