
Fuvest - 1ª fase
Um automóvel, modelo flex, consome 34 litros de gasolina para percorrer 374 km. Quando se opta pelo uso do álcool, o automóvel consome 37 litros deste combustível para percorrer 259 km. Suponha que um litro de gasolina custe R$ 2,20. Qual deve ser o preço do litro do álcool para que o custo do quilômetro rodado por esse automóvel, usando somente gasolina ou somente álcool como combustível, seja o mesmo?
| a) |
R$ 1,00 |
| b) |
R$ 1,10 |
| c) |
R$ 1,20 |
| d) |
R$ 1,30 |
| e) |
R$ 1,40 |
O desempenho do automóvel com gasolina é: .
Com a gasolina a R$ 2,20 o litro, o custo do quilômetro rodado quando o carro usa somente gasolina é de:
Já com álcool, seu desempenho é: .
Se o custo do quilômetro rodado, com o carro usando somente gasolina, deve ser igual ao custo de quando o carro usa somente álcool, o preço do litro do álcool deve ser de:
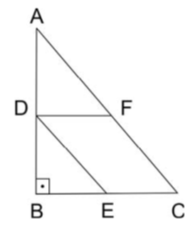
Na figura, o triângulo ABC é retângulo com catetos BC = 3 e AB = 4. Além disso, o ponto D pertence ao cateto , o ponto E pertence ao cateto e o ponto F pertence à hipotenusa , de tal forma que DECF seja um paralelogramo. Se DE = 3/2, então a área do paralelogramo DECF vale
| a) |
|
| b) |
|
| c) |
|
| d) |
|
| e) |
|
A medida da hipotenusa é dada por: .
Como é paralelo a , os triângulos ABC e DBE são semelhantes (critério ângulo-ângulo). Sendo assim:
A área do paralelogramo DECF é dada por:
Tendo em vista as aproximações log102 0,30, log103 0,48, então o maior número inteiro n ,satisfazendo 10n 12418, é igual a
| a) |
424 |
| b) |
437 |
| c) |
443 |
| d) |
451 |
| e) |
460 |
Aplicando logaritmo de base 10 em ambos os lados da desigualdade do enunciado, temos:
Substituindo as aproximações e na última desigualdade acima, temos:
Assim, segue que o maior número inteiro que satisfaz a desigualdade é n = 451.
Os números , , formam uma progressão aritmética de razão r, de tal modo que , , estejam em progressão geométrica. Dado ainda que e , conclui-se que r é igual a
| a) |
|
| b) |
|
| c) |
|
| d) |
|
| e) |
|
Temos a PA , em que . Sendo r a razão dessa progressão, temos ainda , de modo que podemos reescrevê-la como a PA .
Além disso, a seqüência forma uma progressão geométrica, de modo que, substituindo seus termos em função da razão r da PA, temos: PG .
Assim, pela relação da PG:
A opção nos dá , o que contradiz a condição do enunciado de que .
Já a opção nos dá , que é coerente com a condição .
Assim, .
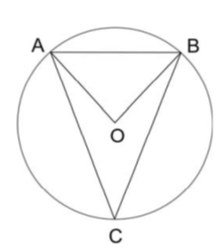
Na figura, os pontos , , pertencem à circunferência de centro e . A reta é perpendicular ao segmento e o ângulo mede radianos. Então, a área do triângulo vale
| a) |
|
| b) |
|
| c) |
|
| d) |
|
| e) |
|
Se o ângulo central mede rad, então o ângulo inscrito determinado pelo mesmo arco mede rad. Vale notar também que o triângulo AOB é equilátero. De fato, esse triângulo é isósceles, uma vez que os lados OA e OB têm medidas iguais ao raio da circunferência. Além disso, como , de modo que os ângulos da base desse triângulo são dados por e . Assim, a reta é reta suporte da altura relativa à base AB do triângulo equilátero AOB e, por conseguinte, a mediatriz relativa a esse lado, de modo que o ponto de intersecção da reta com a corda é ponto médio de .
Como M é ponto médio de , temos três fatos interessantes:
1)2)3) é um lado em comum aos triângulos ACM e BCM
Desse modo, os triângulos ACM e BCM são congruentes pelo caso LAL, de modo que os lados AB e AC possuem a mesma medida. Assim, o triângulo ABC é isósceles de base AB, donde segue que. Assim, a área do triângulo ABC é dada por:
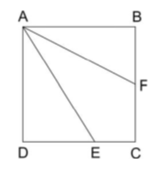
A figura representa um quadrado de lado 1. O ponto está em , mede , o ponto está em e é bissetriz do ângulo . Nessas condições, o segmento mede
| a) |
|
| b) |
|
| c) |
|
| d) |
|
| e) |
|
Seja a medida do ângulo . A partir do triângulo ABF:
Pelo enunciado, como o segmento AF é bissetriz do ângulo , segue que o ângulo é congruente ao ângulo , de modo que o ângulo tem medida igual a . Vale notar que . Assim:
Como e :
A partir da fórmula da tangente do arco duplo:
Desse modo, a medida do segmento DE é dada por:
Racionalizando o denominador da última fração, encontramos .
A função tem como gráfico uma parábola e satisfaz , para todo número real x. Então, o menor valor de ocorre quando x é igual a
| a) |
|
| b) |
|
| c) |
|
| d) |
|
| e) |
|
A função f, tendo como gráfico uma parábola, é uma função do 2º grau e, portanto, é do tipo , para .
Como , para , temos:
, Assim, , para .
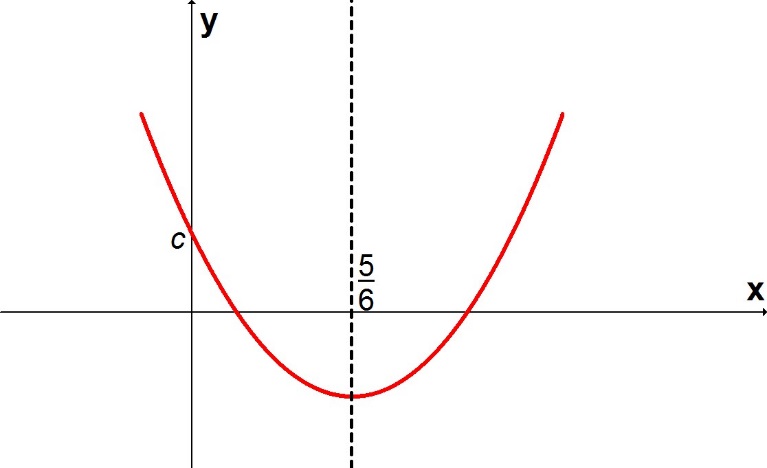
Como o coeficiente do monômio é positivo, essa parábola tem sua concavidade voltada para cima, de modo que seu vértice, nesse caso, corresponde a um ponto de mínimo para a função.
Esse mínimo é atingido na abscissa do vértice, dada por:
Um esboço da parábola, para um valor arbitrário da constante , é apresentado na figura a seguir:
No plano cartesiano x0y, a reta de equação x + y = 2 é tangente à circunferência C no ponto (0,2). Além disso, o ponto (1,0) pertence a C. Então, o raio de C é igual a
| a) |
|
| b) |
|
| c) |
|
| d) |
|
| e) |
|
Seja o centro da circunferência C, e R o seu raio.
Se a circunferência C é tangente à reta r, de equação , no ponto , então o centro da circunferência está sobre a reta s, perpendicular a r em P.
Por outro lado, e são pontos da circunferência, de modo que as distâncias GP e GQ são ambas iguais ao raio R e, portanto, iguais entre si. Esquematizamos a situação na figura a seguir:
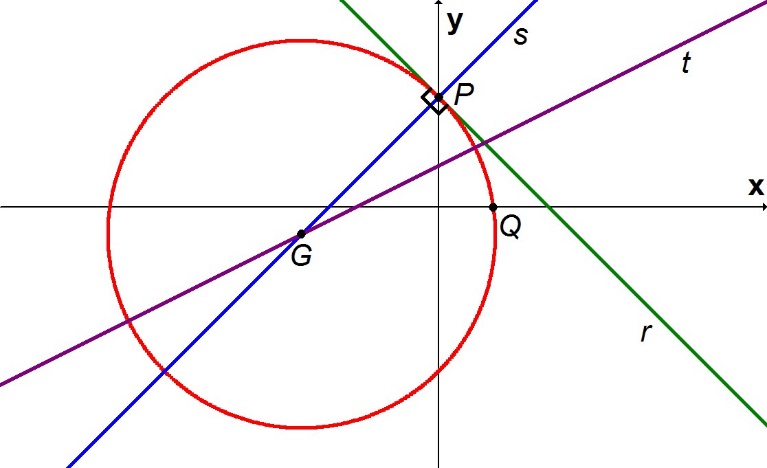
No gráfico, a reta t é o conjunto de todos os pontos equidistantes a P e Q (reta mediatriz do segmento ), sendo o centro G a intersecção entre as retas s e t.
Da equação da reta r, temos: Por outro lado, sendo A equação da reta s é dada por: A equação de t, por sua vez, à qual pertence o ponto G, é dada por:
Assim, as coordenadas do centro G da circunferência são:
O raio da circunferência será dado por:
Maria deve criar uma senha de 4 dígitos para sua conta bancária. Nessa senha, somente os algarismos 1, 2, 3, 4, 5 podem ser usados e um mesmo algarismo pode aparecer mais de uma vez. Contudo, supersticiosa, Maria não quer que sua senha contenha o número 13, isto é, o algarismo 1 seguido imediatamente pelo algarismo 3. De quantas maneiras distintas Maria pode escolher sua senha?
| a) |
551 |
| b) |
552 |
| c) |
553 |
| d) |
554 |
| e) |
555 |
Maria deve utilizar quatro dígitos dentre 1, 2, 3, 4 ou 5. Como cada um dos dígitos pode ser utilizado mais de uma vez, temos, a partir do princípio fundamental da contagem, que o total de senhas possíveis é dado por senhas distintas.
Entretanto, como Maria é supersticiosa, a sequência “13” não pode aparecer em nenhuma posição da senha. Vale notar que existem três situações com essa sequência:
(I) os dois primeiros dígitos são iguais a 1 e 3, respectivamente.
Nesse caso devemos determinar apenas os dois últimos dígitos da senha. Como temos 5 possibilidades para cada dígito, o total de senhas iniciadas por 13 é dado por senhas.
(II) o segundo e terceiro dígitos são iguais a 1 e 3, respectivamente.
Nesse caso devemos determinar o primeiro e quarto dígitos. Novamente, como temos 5 possibilidades para cada um desses dígitos, o total de senhas com dígitos do meio iguais a 1 e 3, nessa ordem, é dado por senhas.
(III) os dois últimos dígitos são iguais a 1 e 3, respectivamente.
Nesse caso devemos determinar os dois primeiros dígitos. Como existem 5 possibilidades para cada um deles, o total de senhas com dígitos finais iguais a 1 e 3, nessa ordem, é dado por senhas.
Vale ressaltar que a senha “1313” aparece tanto no primeiro quanto no último caso, de modo que, tendo sido contada duas vezes, devemos excluí-la uma vez. Assim, o total de senhas onde a sequência “13” aparece ao menos uma vez é dado por senhas.
Desse modo, aplicando o princípio da exclusão, o total de senhas onde a sequência “13” não aparece é dado por .
Uma pirâmide tem como base um quadrado de lado 1, e cada uma de suas faces laterais é um triângulo equilátero. Então, a área do quadrado, que tem como vértices os baricentros de cada uma das faces laterais, é igual a
| a) |
|
| b) |
|
| c) |
|
| d) |
|
| e) |
|
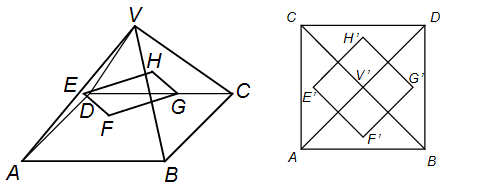
Observe as figuras acima. A primeira mostra a pirâmide ABCDV em questão, com o quadrado EFGH, cuja área se quer determinar. A segunda mostra essa mesma pirâmide projetada na base ABCD, como se estivesse sendo vista de cima, a partir do vértice V.
Como os pontos E, F, G e H são os baricentros das faces laterais da pirâmide, analisando a segunda figura, podemos dizer que tem medida igual a dois terços da distância entre e o segmento , que é igual a .
Logo, e, assim, , que representa a diagonal do quadrado E’F’G’H’, congruente ao quadrado EFGH.
Desse modo, sendo L a medida do lado do quadrado em questão, temos que: .
Portanto, sua área é dada por .