
Fuvest - 1ª fase
Sejam e . A soma dos valores absolutos das raízes da equação é igual a
| a) |
4 |
| b) |
5 |
| c) |
6 |
| d) |
7 |
| e) |
8 |
Temos que:
ou Assim, a soma dos valores absolutos das raízes da equação é igual a:
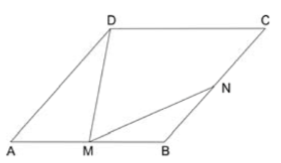
No losango ABCD de lado 1, representado na figura, tem-se que M é o ponto médio de , N é o ponto médio de e . Então, DM é igual a
| a) |
|
| b) |
|
| c) |
|
| d) |
|
| e) |
|
Como M é ponto médio de AB e N é ponto médio de BC, temos que:
AM = BM = BN = NC =
Seja a medida do ângulo , então, é a medida do ângulo .
Aplicando a Lei dos Cossenos no triângulo MBN, temos:
Aplicando agora a Lei dos Cossenos no triângulo ADM, e usando o fato que , temos:
Seja tal que a sequência , , forme, nessa ordem, uma progressão aritmética. Então, é igual a
| a) |
|
| b) |
|
| c) |
|
| d) |
|
| e) |
|
Usando a definição e propriedades de logaritmo, temos que:
Como a sequência (a1, a2, a3) é uma PA, temos que , logo:
Assim, temos que:
Logo:
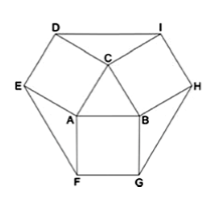
Na figura, o triângulo ABC é equilátero de lado 1, e ACDE, AFGB e BHIC são quadrados. A área do polígono DEFGHI vale
| a) |
|
| b) |
|
| c) |
|
| d) |
|
| e) |
|
De acordo com a figura, temos que:
Assim, a área do polígono DEFGHI pode ser calculada como:
Sejam x e y números reais positivos tais que . Sabendo-se que , o valor de é igual a
| a) |
|
| b) |
|
| c) |
|
| d) |
|
| e) |
|
Como x e y são positivos e , temos que são válidas as igualdades:
Assim:
Por outro lado, da relação fundamental da Trigonometria:
Temos o sistema:
Além disso:
.
Como , temos também que , de modo que:
A esfera ε, de centro O e raio r > 0, é tangente ao plano α. O plano β é paralelo a α e contém O. Nessas condições, o volume da pirâmide que tem como base um hexágono regular inscrito na intersecção de ε com β e, como vértice, um ponto em α, é igual a
| a) |
|
| b) |
|
| c) |
|
| d) |
|
| e) |
|
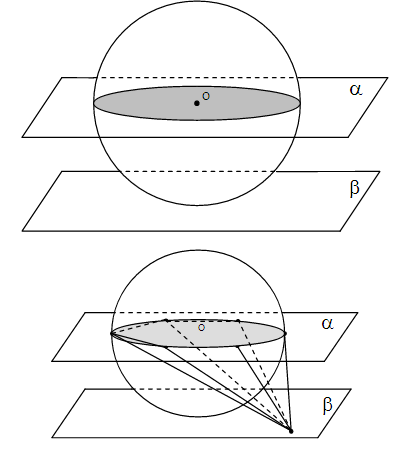
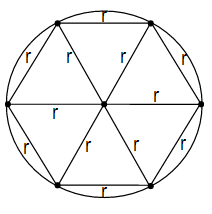
Como o plano contém o centro O, a sua interseção com a esfera é um círculo de raio r; assim a base da pirâmide, que é um hexágono inscrito em um círculo de raio r, tem aresta da base b medindo b = r. Já a altura da pirâmide tem medida igual à distância entre os planos e , que é igual a r. Assim, temos que:
Um dado cúbico, não viciado, com faces numeradas de 1 a 6, é lançado três vezes. Em cada lançamento, anota-se o número obtido na face superior do dado, formando-se uma sequência (a, b, c). Qual é a probabilidade de que b seja sucessor de a ou que c seja sucessor de b?
| a) |
|
| b) |
|
| c) |
|
| d) |
|
| e) |
|
Considere os seguintes eventos:
A: b é sucessor de a
B: c é sucessor de b
Por consequência note que corresponde ao evento “c é sucessor de b e b é sucessor de a”, enquanto corresponde ao evento “b é sucessor de a ou c é sucessor de b”, justamente o evento pedido pelo enunciado.
Assim:
1) Se b é sucessor de a então temos 5 possibilidades em 6 para a (a só não pode ser igual a 6), 1 possibilidade em 6 para b e 6 possibilidades em 6 para c, de modo que .
2) Se c é sucessor de b então temos 6 possibilidades em 6 para a, 5 possibilidades em 6 para b e 1 possibilidade em 6 para c, de modo que .
3) Se b é sucessor de a e c é sucessor de b então temos 4 possibilidades em 6 para a, 1 possibilidade em 6 para b e 1 possibilidade em 6 para c, de modo que .
Desse modo:
No plano cartesiano, os pontos e pertencem à circunferência C. Uma outra circunferência, de centro em , é tangente a C no ponto .
Então, o raio de C vale
| a) |
|
| b) |
|
| c) |
|
| d) |
|
| e) |
|
Sejam e os dois pontos dados, o centro da circunferência C e o centro da outra circunferência. Temos o esquema:
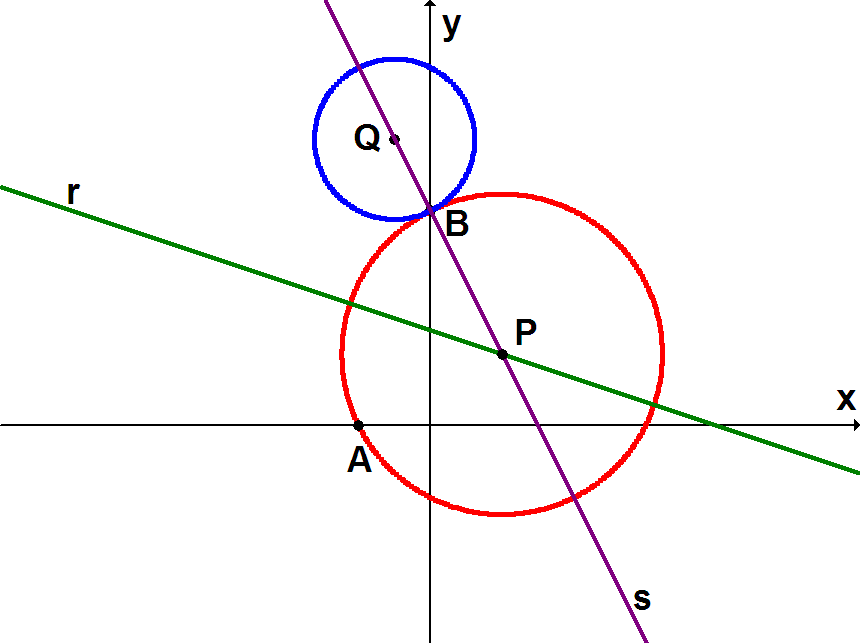
Sendo (raio de C):
Essa equação é a equação da reta mediatriz do segmento , que corresponde ao lugar geométrico dos pontos do plano que equidistam dos pontos A e B. Chamemos tal reta de r.
Por outro lado, os pontos P e Q estão alinhados com o ponto de tangência entre as duas circunferências, que é o ponto B. Assim:
Essa equação corresponde à equação da reta determinada pelos pontos B e Q, a qual chamaremos de s.
A interseção das retas r e s é o centro P da circunferência C:
A medida do raio R é igual à distância PB:
Seja , em que a, b e c são números reais. A imagem de f é a semirreta ]-1, [ e o gráfico de f intercepta os eixos coordenados nos pontos (1,0) e (0,-3/4). Então, o produto abc vale
| a) |
4.
|
| b) |
2.
|
| c) |
0.
|
| d) |
-2.
|
| e) |
-4.
|
Como a imagem da função é a semirreta , segue que , uma vez que para qualquer x real.
O gráfico de f(x) passa por (1;0) e (0;-3/4). Assim:
Desse modo, a = -1, b = 2 e c = -2, donde segue que .
Um sólido branco apresenta as seguintes propriedades:
I. É solúvel em água.
II. Sua solução aquosa é condutora de corrente elétrica.
III. Quando puro, o sólido não conduz corrente elétrica.
IV. Quando fundido, o líquido puro resultante não conduz corrente elétrica.
Considerando essas informações, o sólido em questão pode ser
| a) |
sulfato de potássio. |
| b) |
hidróxido de bário. |
| c) |
platina. |
| d) |
ácido cis-butenodioico. |
| e) |
polietileno. |
a) e b) Incorretas. O sulfato de potássio (K2SO4) e o hidróxido de bário (Ba(OH)2) são solúveis em água e, por serem substâncias iônicas, sofrem dissociação em água, tornando suas soluções aquosas condutoras de corrente elétrica. Além disso, os compostos iônicos no estado sólido não conduzem corrente, porém conduzem no estado líquido (fundido).
c) Incorreta. A platina (Pt) é um metal sólido à temperatura ambiente, sendo insolúvel em água. Além disso, conduz corrente elétrica tanto no estado sólido quanto no estado líquido.
d) Correta. O ácido cis-butenodióico é um composto molecular que possui duas carboxilas na posição cis, o que torna essa molécula polar. Por fazer ligação de hidrogênio com a água, torna-se solúvel nesse solvente e possui dois hidrogênios ionizáveis, portanto sua solução aquosa conduz corrente elétrica. Já na forma de líquido puro, não conduz corrente elétrica, pois ao se fundir não sofre ionização.
Figura: Ácido cis-butenodióico
e) Incorretas. O polietileno é um polímero formado apenas por carbono e hidrogênio e é apolar, portanto insolúvel em água. Essa substância é formada apenas por ligações covalentes e não sofre ionização em água e nem ao ser fundido, portanto não conduz corrente elétrica nos estados líquido, sólido ou dissolvido em solvente.
Figura: Polietileno