
Unicamp - 2ª fase - Matemática e Inglês
O transporte de carga ao porto de Santos é feito por meio de rodovias, ferrovias e dutovias. A tabela abaixo fornece alguns dados relativos ao transporte ao porto no primeiro semestre de 2007 e no primeiro semestre de 2008, indicando claramente o aumento da participação percentual do transporte ferroviário nesse período. Com base nos dados da tabela, responda às questões abaixo.
|
Meio de transporte |
Participação no total transportado ao porto |
Carga transportada (em milhões de toneladas) |
||
|
2007 |
2008 |
2007 |
2008 |
|
|
Ferroviário |
18% |
24% |
6,8 |
8,8 |
|
Rodoviário |
77% |
29,1 |
||
|
Dutoviário |
||||
a) Determine a carga total (em milhões de toneladas) transportada ao porto no primeiro semestre de 2007. Calcule também quantas toneladas foram transportadas por dutos no primeiro semestre de 2007.
b) Sabendo que, no primeiro semestre de 2008, foram transportadas por rodovias 2,7 milhões de toneladas a menos do que o valor registrado pelo mesmo meio de transporte no primeiro semestre de 2007, calcule a participação percentual do transporte rodoviário no primeiro semestre de 2008.
a)
b) 72%
Uma lâmpada incandescente de 100 W custa R$ 2,00. Já uma lâmpada fluorescente de 24 W, que é capaz de iluminar tão bem quanto a lâmpada incandescente de 100 W, custa R$ 13,40. Responda às questões abaixo, lembrando que, em uma hora, uma lâmpada de 100 W consome uma quantidade de energia equivalente a 100 Wh, ou 0,1 kWh. Em seus cálculos, considere que 1 kWh de energia custa R$ 0,50.
a) Levando em conta apenas o consumo de energia, ou seja, desprezando o custo de aquisição da lâmpada, determine quanto custa manter uma lâmpada incandescente de 100 W acesa por 750 horas. Faça o mesmo cálculo para uma lâmpada fluorescente de 24 W.
b) Para iluminar toda a sua casa, João comprou e instalou apenas lâmpadas fluorescentes de 24 W. Fernando, por sua vez, comprou e instalou somente lâmpadas incandescentes de 100 W para iluminar sua casa. Considerando o custo de compra de cada lâmpada e seu consumo de energia, determine em quantos dias Fernando terá gasto mais com iluminação que João. Suponha que cada lâmpada fica acesa 3 horas por dia. Suponha, também, que as casas possuem o mesmo número de lâmpadas.
a) R$ 37,50 (incandescente) e R$ 9,00 (fluorescente)
b) mais do que 100 dias
Em uma bandeja retangular, uma pessoa dispôs brigadeiros formando n colunas, cada qual com m brigadeiros, como mostra a figura abaixo. Os brigadeiros foram divididos em dois grupos. Os que estavam mais próximos das bordas da bandeja foram postos em forminhas azuis, enquanto os brigadeiros do interior da bandeja foram postos em forminhas vermelhas.
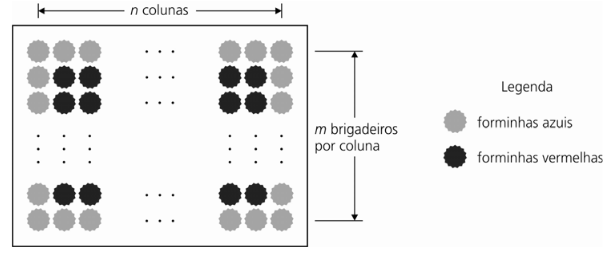
a) Sabendo que m = 3n/4 e que a pessoa gastou o mesmo número de forminhas vermelhas e azuis, determine o número de brigadeiros da bandeja.
b) Se a pessoa compra a massa do brigadeiro já pronta, em latas de 1 litro, e se cada brigadeiro, antes de receber o chocolate granulado que o cobre, tem o formato de uma esfera de 2 cm de diâmetro, quantas latas ela tem que comprar para produzir 400 brigadeiros? (Dica: lembre-se de que 1 litro corresponde a 1000 cm3.)
a) 48 brigadeiros
b) 2 latas
Três candidatos A, B e C concorrem à presidência de um clube. Uma pesquisa apontou que, dos sócios entrevistados, 150 não pretendem votar. Dentre os entrevistados que estão dispostos a participar da eleição, 40 sócios votariam apenas no candidato A, 70 votariam apenas em B, e 100 votariam apenas no candidato C. Além disso, 190 disseram que não votariam em A, 110 disseram que não votariam em C, e 10 sócios estão na dúvida e podem votar tanto em A como em C, mas não em B. Finalmente, a pesquisa revelou que 10 entrevistados votariam em qualquer candidato. Com base nesses dados, pergunta-se:
a) Quantos sócios entrevistados estão em dúvida entre votar em B ou em C, mas não votariam em A? Dentre os sócios consultados que pretendem participar da eleição, quantos não votariam em B?
b) Quantos sócios participaram da pesquisa? Suponha que a pesquisa represente fielmente as intenções de voto de todos os sócios do clube. Escolhendo um sócio ao acaso, qual a probabilidade de que ele vá participar da eleição mas ainda não tenha se decidido por um único candidato?
(Sugestão: utilize o diagrama de Venn fornecido abaixo)
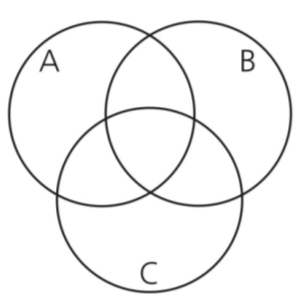
a) Levando em consideração apenas as informações do , podemos preencher o diagrama de Venn abaixo:
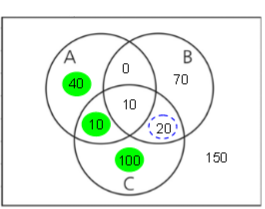
Logo, o número de sócios entrevistados que estão em dúvida entre votar em B ou C, mas não em A, é igual a 20 (destacado em azul tracejado). E o número de sócios que não votariam em B é igual a 150 (destacado em verde hachurado).
b) 400 ; 10%
Duas locadoras de automóveis oferecem planos diferentes para a diária de um veículo econômico. A locadora Saturno cobra uma taxa fixa de R$ 30,00, além de R$ 0,40 por quilômetro rodado. Já a locadora Mercúrio tem um plano mais elaborado: ela cobra uma taxa fixa de R$ 90,00 com uma franquia de 200 km, ou seja, o cliente pode percorrer 200 km sem custos adicionais. Entretanto, para cada km rodado além dos 200 km incluídos na franquia, o cliente deve pagar R$ 0,60.
a) Para cada locadora, represente no gráfico abaixo a função que descreve o custo diário de locação em termos da distância percorrida no dia.
b) Determine para quais intervalos cada locadora tem o plano mais barato. Supondo que a locadora Saturno vá manter inalterada a sua taxa fixa, indique qual deve ser seu novo custo por km rodado para que ela, lucrando o máximo possível, tenha o plano mais vantajoso para clientes que rodam quaisquer distâncias.
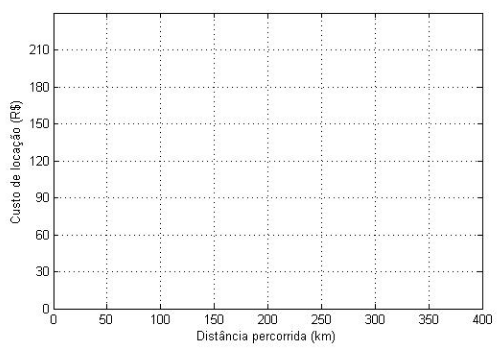
a) Gráfico:
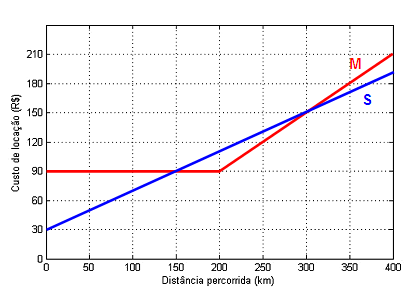
b) Se ou se temos e, portanto, a locadora mais vantajosa é a Saturno.
Se , e, portanto, a locadora mais vantajosa é a Mercúrio.
Se ou , e, portanto, a escolha é indiferente.
Novo custo: R$ 0,30 por km.
Um casal convidou seis amigos para assistirem a uma peça teatral. Chegando ao teatro, descobriram que, em cada fila da sala, as poltronas eram numeradas em ordem crescente. Assim, por exemplo, a poltrona 1 de uma fila era sucedida pela poltrona 2 da mesma fila, que, por sua vez, era sucedida pela poltrona 3, e assim por diante.
a) Suponha que as oito pessoas receberam ingressos com numeração consecutiva de uma mesma fila e que os ingressos foram distribuídos entre elas de forma aleatória. Qual a probabilidade de o casal ter recebido ingressos de poltronas vizinhas?
b) Suponha que a primeira fila do teatro tenha 8 cadeiras, a segunda fila tenha 2 cadeiras a mais que a primeira, a terceira fila tenha 2 cadeiras a mais que a segunda e assim sucessivamente até a última fila. Determine o número de cadeiras da sala em função de n, o número de filas que a sala contém. Em seguida, considerando que a sala tem 144 cadeiras, calcule o valor de n.
a)
b) ;
O sistema de ar condicionado de um ônibus quebrou durante uma viagem. A função que descreve a temperatura (em graus Celsius) no interior do ônibus em função de t, o tempo transcorrido, em horas, desde a quebra do ar condicionado, é
,
onde T0 é a temperatura interna do ônibus enquanto a refrigeração funcionava, e Text é a temperatura externa (que supomos constante durante toda a viagem). Sabendo que T0 = 21 °C e Text = 30 °C, responda às questões abaixo.
a) Calcule a temperatura no interior do ônibus transcorridas 4 horas desde a quebra do sistema de ar condicionado. Em seguida, esboce abaixo o gráfico de T(t).
b) Calcule o tempo gasto, a partir do momento da quebra do ar condicionado, para que a temperatura subisse 4 °C. Se necessário, use , e .
a) Como e , temos:
Para , temos:
O gráfico é dado por:
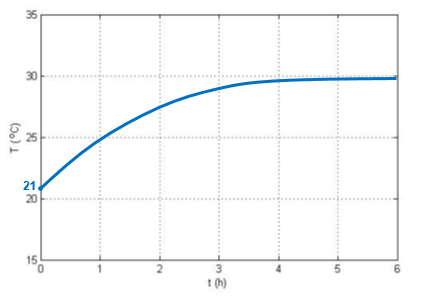
b) Queremos encontrar de modo que . Assim, fazemos:
Embora acreditemos que não seja necessário, tal resposta também poderia ser expressa como 1 h, 2 min e 24 s.
Pedro precisa comprar x borrachas, y lápis e z canetas. Após fazer um levantamento em duas papelarias, Pedro descobriu que a papelaria A cobra R$ 23,00 pelo conjunto de borrachas, lápis e canetas, enquanto a papelaria B cobra R$ 25,00 pelo mesmo material. Em seu levantamento, Pedro descobriu que a papelaria A cobra R$ 1,00 pela borracha, R$ 2,00 pelo lápis e R$ 3,00 pela caneta e que a papelaria B cobra R$ 1,00 pela borracha, R$ 1,00 pelo lápis e R$ 4,00 pela caneta.
a) Forneça o número de lápis e de borrachas que Pedro precisa comprar em função do número de canetas que ele pretende adquirir.
b) Levando em conta que x ≥ 1, y ≥ 1 e z ≥ 1, e que essas três variáveis são inteiras, determine todas as possíveis quantidades de lápis, borrachas e canetas que Pedro deseja comprar.
a)
b) As triplas ordenadas (x, y, z) que representam o número de lápis, borrachas e canetas que Pedro pode comprar nas condições apresentadas são (12, 1, 3), (7, 2, 4) e (2, 3, 5).
A figura a seguir mostra um sapo de origami, a arte japonesa das dobraduras de papel.

A figura abaixo mostra o diagrama usado para a confecção do sapo, na qual se utiliza um retângulo de papel com arestas iguais a c e 2c. As linhas representam as dobras que devem ser feitas. As partes destacadas correspondem à parte superior e à pata direita do sapo, e são objeto das perguntas a seguir.
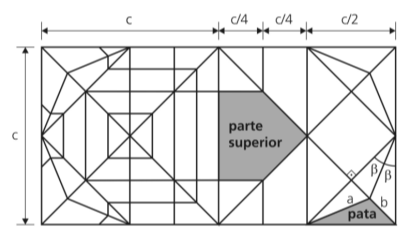
a) Quais devem ser as dimensões, em centímetros, do retângulo de papel usado para confeccionar um sapo cuja parte superior tem área igual a 12 cm2?
b) Qual a razão entre os comprimentos das arestas a e b da pata direita do sapo?
a)
b)
Uma caixa d’água tem o formato de um tronco de pirâmide de bases quadradas e paralelas, como mostra a figura abaixo, na qual são apresentadas as medidas referentes ao interior da caixa.
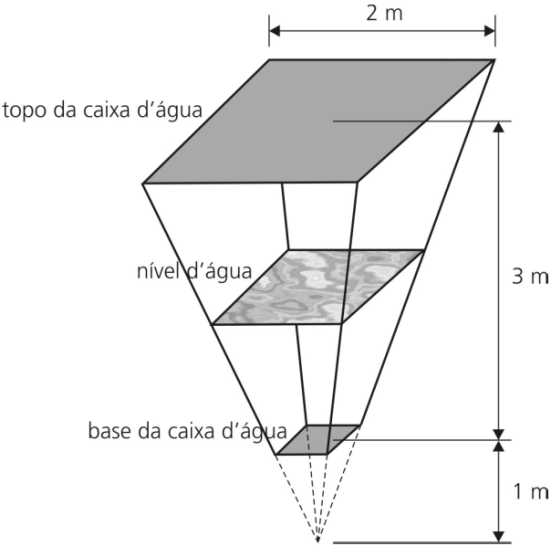
a) Qual o volume total da caixa d’água?
b) Se a caixa contém (13/6) m3 de água, a que altura de sua base está o nível d’água?
a) Observe a figura abaixo:
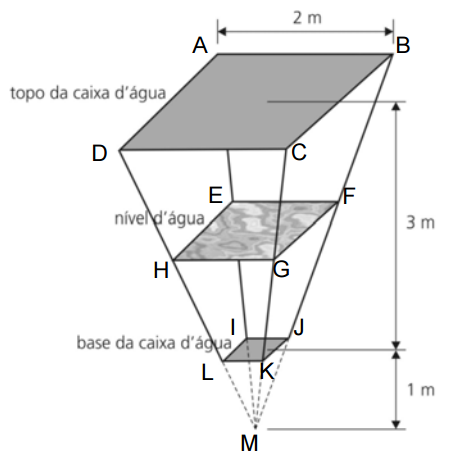
O volume total da caixa d'água é dado por:
Como as pirâmides ABCDM e IJKLM são semelhantes, temos:
Logo, o volume total da caixa d'água é:
b)
O volume da pirâmide EFGHM é dado por:
Seja h a altura da água em relação à base da caixa d´água. Como as pirâmides EFGHM e IJKLM são semelhantes, temos: