
Unesp - 1ª fase
Define-se a intensidade de uma onda (I) como potência transmitida por unidade de área disposta perpendicularmente à direção de propagação da onda. Porém, essa definição não é adequada para medir nossa percepção de sons, pois nosso sistema auditivo não responde de forma linear à intensidade das ondas incidentes, mas de forma logarítmica. Define-se, então, nível sonoro (β) como, ,sendo β dado em decibel (dB) e I0 = 10–12 W/m2.
Supondo que uma pessoa, posicionada de forma que a área de de um de seus tímpanos esteja perpendicular à direção de propagação da onda, ouça um som contínuo de nível sonoro igual a 60 dB durante 5,0 s, a quantidade de energia que atingiu seu tímpano nesse intervalo de tempo foi
| a) |
3,0 × 10–10 J.
|
| b) |
1,8 × 10–14 J.
|
| c) |
3,0 × 10–12 J.
|
| d) |
6,0 × 10–9 J.
|
| e) |
1,8 × 10–9 J.
|
Como foi dado o nível sonoro, podemos calcular a intensidade sonora no ouvido:
Como a função logaritmo é a inversa da exponencial e a base para cálculo de nível sonoro é a base 10, temos:
Sabendo a intensidade, podemos calcular a potência :
sendo a área do tímpano. Assim:
Por fim, calculemos a energia pedida pela relação:
Para obter experimentalmente a curva da diferença de potencial em função da intensidade da corrente elétrica para uma lâmpada, um aluno montou o circuito a seguir. Colocando entre os pontos A e B resistores com diversos valores de resistência, ele obteve diferentes valores de e de para a lâmpada.
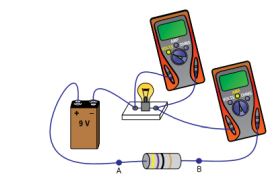
Considerando que a bateria de 9,0 V, os aparelhos de medida e os fios de ligação sejam ideais, quando o aluno obteve as medidas e , a resistência do resistor colocado entre os pontos A e B era de
| a) |
a)
|
| b) |
b)
|
| c) |
c)
|
| d) |
d)
|
| e) |
e)
|
Como a lâmpada está em série com o resistor (figura abaixo), temos que a diferença de potencial fornecida pela bateria corresponde a soma das diferenças de potencial na lâmpada com a diferença de potencial no resistor: a d.d.p. na lâmpada corresponde a indicação do voltímetro.
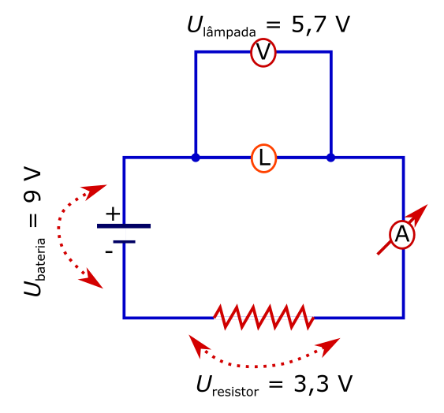
Como a lâmpada está em série com o resistor a intensidade da corrente elétrica é a mesma, assim, para o resistor:
O ibuprofeno é uma medicação prescrita para dor e febre, com meia-vida de aproximadamente 2 horas. Isso significa que, por exemplo, depois de 2 horas da ingestão de 200 mg de ibuprofeno, permanecerão na corrente sanguínea do paciente apenas 100 mg da medicação. Após mais 2 horas (4 horas no total), apenas 50 mg permanecerão na corrente sanguínea e, assim, sucessivamente.
Se um paciente recebe 800 mg de ibuprofeno a cada 6 horas, a quantidade dessa medicação que permanecerá na corrente sanguínea na 14ª hora após a ingestão da primeira dose será
| a) |
6,25 mg.
|
| b) |
12,50 mg.
|
| c) |
537,50 mg.
|
| d) |
114,28 mg.
|
| e) |
456,25 mg.
|
Podemos notar que a função que descreve a quantidade de massa do ibuprofeno em função do tempo, para um ciclo de 6 horas do medicamento é do tipo:
Onde
é a massa inicial de ibuprofeno, k uma constante real e t varia entre 0 e 6, tendo em vista que o paciente recebe uma nova dose a cada 6 horas. Note que, o tempo de meia vida é de duas horas, logo:
Logo, a função é:
Vamos analisar quanto de ibuprofeno permanecerá na corrente sanguínea após o primeiro ciclo de 6 horas do medicamento.
Permanecerá na corrente após 6 horas, 100 mg. Ao ingerir uma nova dose de 800 mg, o paciente terá em sua corrente:
Analogamente, após mais 6 horas, ou seja, após a 12ª hora de ingestão da primeira dose, teremos:
Por fim, após ingerir mais 800 mg, o paciente terá em sua corrente,
E após duas horas desta última ingestão, ou seja, após a 14ª hora, permanecerá em sua corrente sanguínea:
A figura indica um trapézio ABCD no plano cartesiano.
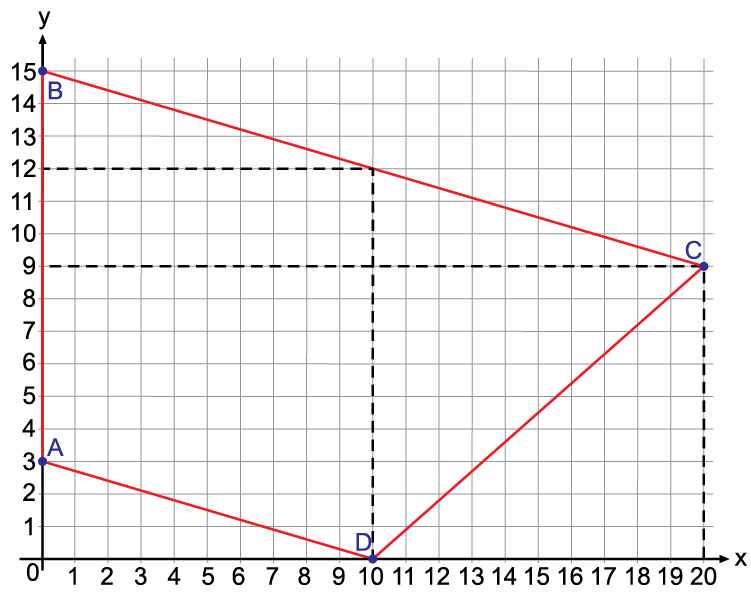
A área desse trapézio, na unidade quadrada definida pelos eixos coordenados, é igual a
| a) |
155.
|
| b) |
160.
|
| c) |
175.
|
| d) |
180.
|
| e) |
170.
|
1ª Resolução:
Para determinar a área do trapézio podemos calcular a área do retângulo e depois subtrair a área dos triângulos.
<** DIAGRAMA VETORIAL NÃO CONVERTIDO **>
2ª Resolução:
Temos os pontos,
, a área do trapézio pode ser calculada somando as áreas dos triângulos ABC e CDA.
Lembrando que a área de um triângulo de vértices
é dada por
em que
Assim, para o triângulo ABC:
Calculando o determinante pela regra de Sarrus:
Logo,
Agora, calculando a área do triângulo CDA:
Calculando o determinante pela regra de Sarrus:
Logo,
Portanto
Os estudantes 1, 2 e 3 concorreram a um mesmo cargo da diretoria do grêmio de uma faculdade da UNESP, sendo que 1 obteve 6,25% do total de votos que os três receberam para esse cargo. Na figura, a área de cada um dos três retângulos representa a porcentagem de votos obtidos pelo candidato correspondente. Juntos, os retângulos compõem um quadrado, cuja área representa o total dos votos recebidos pelos três candidatos.
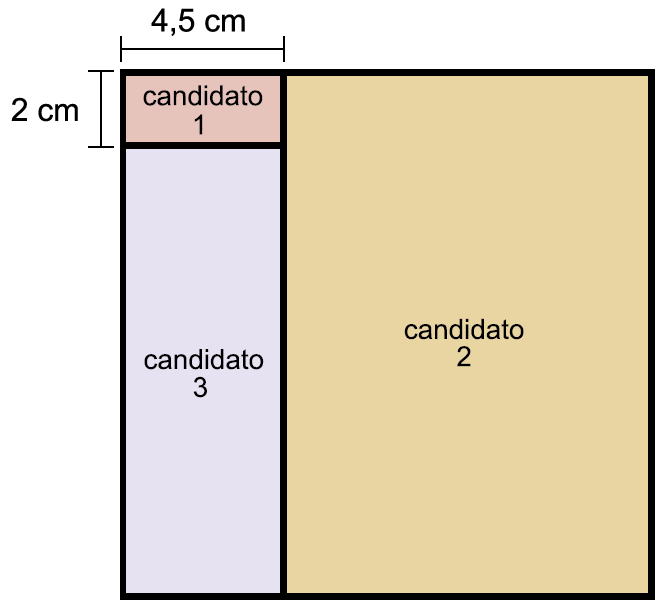
Do total de votos recebidos pelos três candidatos, o candidato 2 obteve
| a) |
62,00%.
|
| b) |
62,50%.
|
| c) |
61,75%.
|
| d) |
62,25%.
|
| e) |
62,75%.
|
Sabe-se que a área de cada um dos retângulos corresponde à porcentagem dos votos do respectivo candidato com relação ao total.
A partir da figura, concluímos que a área relativa ao candidato 1 é
Como esta área corresponde a 6,25% da área total, temos
Como os retângulos formam, juntos, um quadrado de área
, temos que seu lado deve ser
Estamos interessados em encontrar a porcentagem dos votos relativo ao candidato 2. Para isto, vamos calcular a área do retângulo associado a este candidato. Pela figura, observamos que este retângulo tem dimensões
e
.
Logo, sua área é
.
Assim,
.
Dois dos materiais mais utilizados para fazer pistas de rodagem de veículos são o concreto e o asfalto. Uma pista nova de concreto reflete mais os raios solares do que uma pista nova de asfalto; porém, com os anos de uso, ambas tendem a refletir a mesma porcentagem de raios solares, conforme mostram os segmentos de retas nos gráficos.
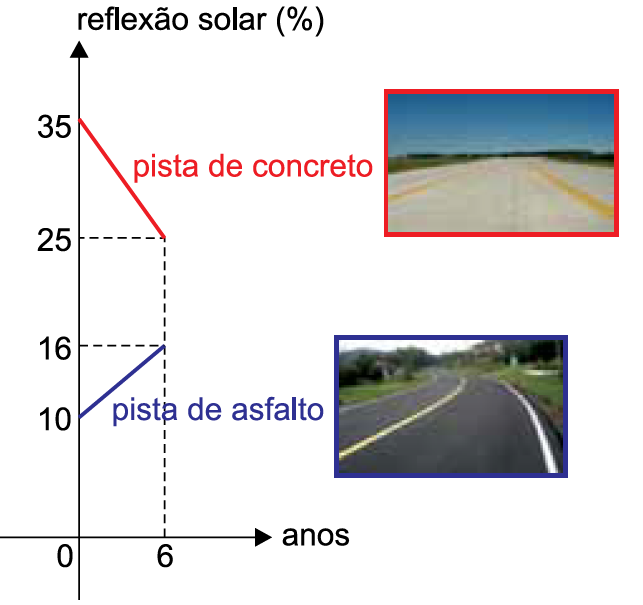
(www.epa.gov. Adapado)
Mantidas as relações lineares expressas nos gráficos ao longo dos anos de uso, duas pistas novas, uma de concreto e outra de asfalto, atingirão pela primeira vez a mesma porcentagem de reflexão dos raios solares após
| a) |
9,625 anos.
|
| b) |
10,025 anos.
|
| c) |
8,225 anos.
|
| d) |
9,375 anos.
|
| e) |
10,175 anos.
|
Para encontrar o ponto em que as pistas terão a mesma porcentagem de reflexão, precisamos encontrarmos a intersecção das retas esboçadas no gráfico. Para isso podemos primeiramente determiná-las:
Chamemos de r e s as retas que determinam a pista de concreto e asfalto, respectivamente.
Sabemos que a reta s passa pelos pontos (0, 35) e (6, 25), então, seja r:
, substituindo os pontos temos que:
e
De forma análoga, sabemos que r passa pelos pontos (0,10) e (6,16), então seja s:
, substituindo os pontos temos que:
e
Portanto,
e
Agora, para determinar
basta encontrarmos
:
A sequência de figuras, desenhadas em uma malha quadriculada, indica as três primeiras etapas de formação de um fractal. Cada quadradinho dessa malha tem área de 1 cm².
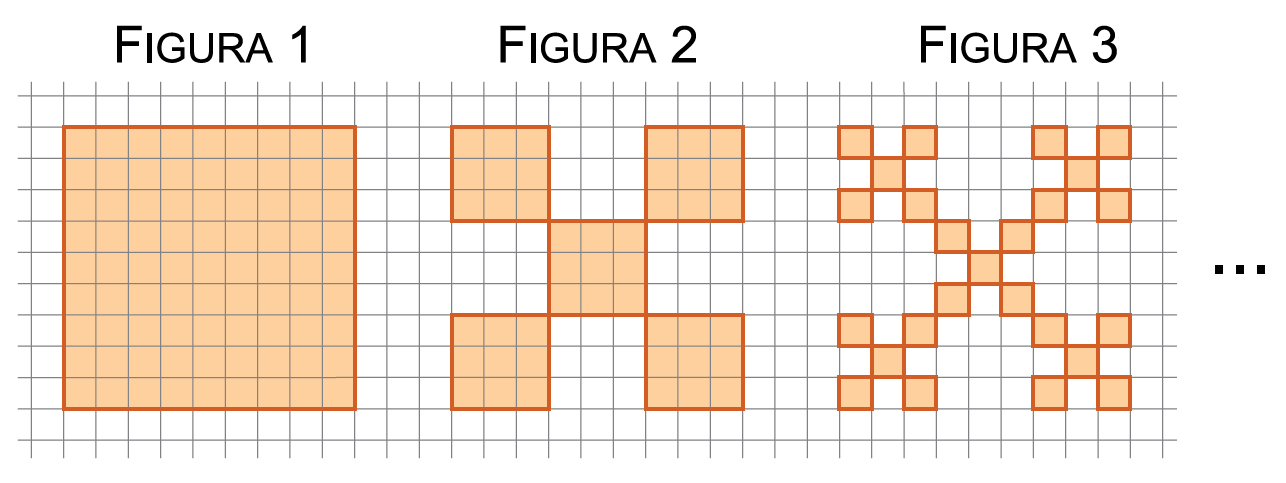
Dado que as áreas das figuras, seguindo o padrão descrito por esse fractal, formam uma progressão geométrica, a área da figura 5, em cm², será igual a
| a) |
|
| b) |
|
| c) |
|
| d) |
|
| e) |
|
Primeiramente, lembramos que a fórmula do termo geral de uma progressão geométrica é dada por:
onde
é o n-ésimo termo da P.G.,
é o primeiro e
é sua razão.
Da figura notamos que
e
. A partir do enunciado podemos garantir que a sequência das áreas forma uma progressão geométrica, logo sua razão deve ser:
Utilizando a fórmula do termo geral para encontrar a área do quinto termo da sequência, obtemos:
Os pontos e pertencem a uma circunferência centrada na origem do plano cartesiano. também é ponto de intersecção da circunferência com o eixo y.
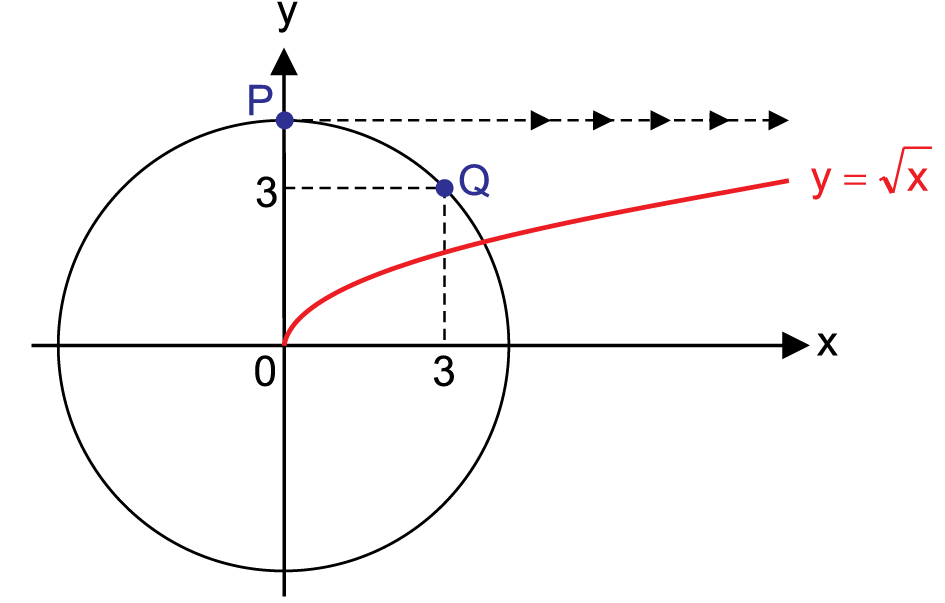
Considere o ponto R, do gráfico de , que possui ordenada y igual à do ponto P. A abscissa x de R é igual a
| a) |
9.
|
| b) |
16.
|
| c) |
12.
|
| d) |
15.
|
| e) |
18.
|
Como o ponto
pertence à circunferência, podemos obter seu raio
pelo Teorema de Pitágoras:
Assim, determinamos o ponto
. Queremos encontrar a abscissa do ponto R que seria a interseção do gráficos da função
e da reta
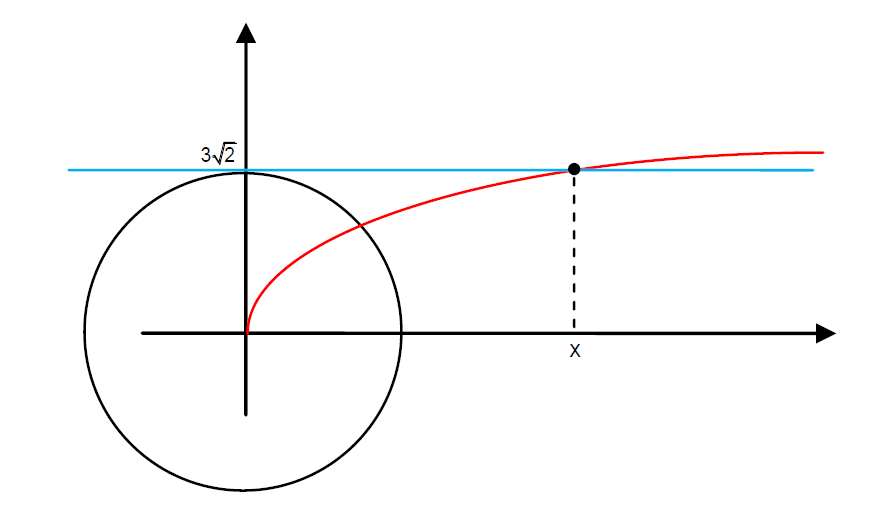
Logo,
Como
, temos
A figura indica os gráficos das funções I, II e III. Os pontos A (72º, 0,309), B( , – 0,309) e C( , 0,309) são alguns dos pontos de intersecção dos gráficos.
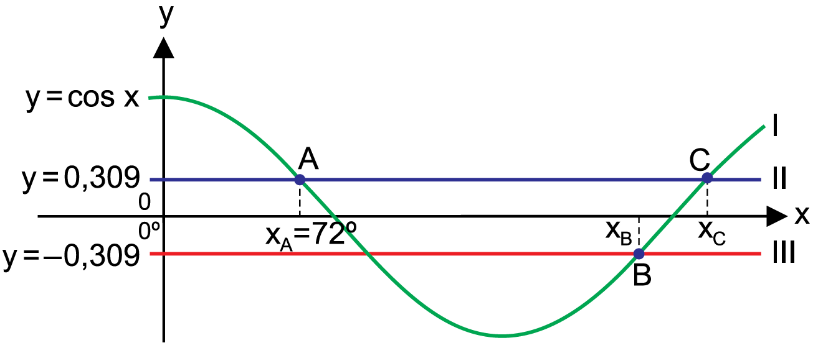
Nas condições dadas, é igual a
| a) |
538º
|
| b) |
460º
|
| c) |
540º
|
| d) |
488º
|
| e) |
432º
|
1ª Solução:
Buscamos as abscissas dos pontos B e C, pertencentes à função
, como apresentado no gráfico:
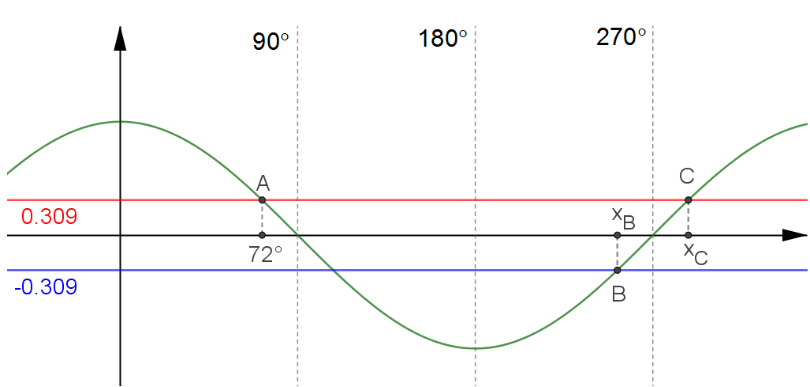
Para melhorar a localização, traçamos retas verticais para a separação por quadrantes, logo, temos que
,
e
.
Passando os pontos para a circunferência trigonométrica temos as seguintes simetrias, de acordo com os quadrantes.
Então podemos concluir que:
Buscamos a soma:
.
2ª Solução:
Partindo da soma temos que:
Pela fórmula de Prostaférese:
Logo,
Daí, como
e
, temos que:
Logo,
Só nos resta uma possibilidade:
Daí, como
e
, temos que:
Logo,
Renata escolhe aleatoriamente um número real de a e diferente de zero, denotando-o por . Na reta real, o intervalo numérico que necessariamente contém o número é
| a) |
|
| b) |
|
| c) |
|
| d) |
|
| e) |
|
Pelas informações do enunciado, temos que ou .
Note que analisar a expressão é equivalente a analisar a expressão .
Analisando-a para o primeiro caso, temos:
.
Multiplicando os dois lados da desigualdade por 2, temos que
.
Finalmente, subtraindo 1 de ambos os lados da desigualdade, obtemos:
Fazendo o procedimento análogo para o segundo caso, temos:
Logo,
ou
Tal solução é representada pela união dos intervalos abaixo:
