
Questão 4 1ª fase
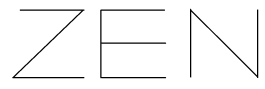
Poema ZEN, Pedro Xisto, 1966.
Diagrama referente ao poema ZEN.
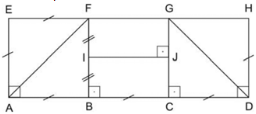
Observe as figuras acima e assinale a alternativa correta.
| a) |
a) O equilíbrio e a harmonia do poema ZEN são elementos típicos da produção poética brasileira da década de 1960. O perímetro do triângulo ABF, por exemplo, é igual ao perímetro do retângulo BCJI. |
| b) |
b) O equilíbrio e a harmonia do poema ZEN podem ser observados tanto no conteúdo semântico da palavra por ele formada quanto na simetria de suas formas geométricas. Por exemplo, as áreas do triângulo ABF e do retângulo BCJI são iguais. |
| c) |
c) O poema ZEN pode ser considerado concreto por apresentar proporções geométricas em sua composição. O perímetro do triângulo ABF, por exemplo, é igual ao perímetro do retângulo BCGF. |
| d) |
d) O concretismo poético pode utilizar proporções geométricas em suas composições. No poema ZEN, por exemplo, a razão entre os perímetros do trapézio ADGF e do retângulo ADHE é menor que 7/10.
|
| e) |
e) Augusto dos Anjos e Manuel Bandeira são representantes do concretismo poético, que utiliza proporções geométricas em suas composições. No poema ZEN, por exemplo, a razão entre as áreas do triângulo DHG e do retângulo ADHE é 1/6
|
Da figura referente ao poema, note que podemos “retirar” a palavra ZEN:
Considere o diagrama matemático fornecido no enunciado:
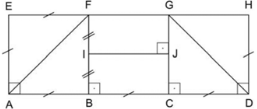
a) Incorreta. O poema se refere ao concretismo brasileiro. A principal característica típica deste movimento era produzir poesias de caráter visual, ocupando o espaço do papel em que forma e conteúdo não existissem, no entanto, perímetro do triângulo ABF é dado por . O perímetro do retângulo BCJI é dado por BC + CJ + JI + IB = 2(AB) + (AB) = 3(AB), logo, os perímetros não são iguais.
b) Correta. A simetria das formas é comprovada matematicamente e o sentido da palavra zen remete ao zen-budismo, tradição oriental em que se valoriza o equilíbrio entre corpo e mente, entre ser e universo, buscando-se a harmonia existencial. Além disso, a área do triângulo ABF é dada por , enquanto a área do retângulo BCJI é dada por , ou seja, elas são iguais.
c) Incorreta. Proporções geométricas não são o suficiente para definir um poema como concreto. São necessárias palavras, a matéria prima da poesia. Adicionalmente, o perímetro do retângulo BCGF é dado por BC + CG + GF + FB = 4(AB), que é diferente do perímetro de ABF, já calculado na alternativa A e cujo valor é .
d) Incorreta. O perímetro do trapézio ADGF é dado por enquanto o perímetro do retângulo ADHE é dado por 8(AB). Assim, a razão entre seus perímetros é , ou seja, a razão é maior que .
e) Incorreta. A área do triângulo DHG é dada por , enquanto a área do retângulo ADHE é dada por . Assim, a razão entre suas áreas é . No entanto, Augusto dos Anjos é um poeta difícil de ser enquadrado em algum movimento literário devido à sua singularidade, mas compôs seus versos no período conhecido por Pré-Modernismo. Já Manuel Bandeira inicia sua carreira literária com produções parnasianas, e em 1922 é já celebrado como poeta moderno, tendo seus versos declamados na semana de Arte Moderna de 1922. A partir de então é enquadrado como poeta Modernista, apesar de pessoalmente não gostar do rótulo. Assim, os poetas citados não são representantes do concretismo.